Growth rate is how much a quantity varies with interval of time expressed as a percentage. In business and financial matters, rates of growth indicate the speed of an important indicator sales, revenue, or an investment value to rise or fall between periods. To illustrate, the revenue of Amazon increased by 12% temporarily between 2024 and 2025 due to the sustained growth of revenue to the tune of $638.0 billion in 2024 to $716.9 billion in 2025.
Growth rates are used to track the performance and give insights into the future and trends. A slowing-down represents growth, lower growth if the rate of growth is positive, expansion, higher sales or profits for instance, as well as, negative rates, represent contraction. An example is the revenue growth rate, which is an immediate indication of the health of a company and its attractiveness to investors since it tells how much sales grew in a year. Raw values become percentage changes that are related to growth rates in data analysis making comparisons between time or comparisons between firms easier.
Basic Growth Rate Percentage
The simplest growth rate formula compares the change to the original value. In general:
- Absolute change = New value − Original value
- Growth rate = Absolute change/Original value
- Percentage growth = Growth rate * 100%.
In other words:
Growth Rate (%) = [(Final Value – Initial Value) / Initial Value]*100%.Steps to calculate basic growth rate:
- Find the difference: Determine the difference between the initial starting point and the final point. This will provide the change that is absolute.
- Divide by original: Divide that difference by the original value. This results in the decimal growth.
- Convert to a percentage: Multiply by 100 to get a % rate.
Example: Given that the number of students in a school per year was 402 in the previous year and 489 this year. The change in absolute terms is 489-402=87 students. Dividing by 402 gives 0.2164, or 21.64% growth. That is, (489-402)/402= 0.2164, then x100. This informs us that the student population increased by 21.6%.
This process can be applied to any one-period change: monthly change, quarterly change, annual change. As an example, when the sales of a product in Q1 were 50,000 and in Q2, the sales were 60000, the growth rate would be (60,000-50,000)/50,000 x 100 = 20%. Negative result only implies a fall, like when the sales dropped to 40,000 by a margin of 50,000, the growth rate is -20%.
You may also like: Doge Software Licenses Audit
Average Growth Rates (Arithmetic Mean)
Occasionally, it is useful for you to have the average growth per period across numerous years (or months) without growing. The average growth rates according to the level of growth within each year are termed the average annual growth rate (AAGR). The formula is:
AAGR = (g₁ + g₂ + … + gₙ) / nIn which g is the growth by year.
Calculations to determine the average growth rate:
- Step 1: The growth rate of each period is computed using the simple formula. To compute the value – Value-1)/Value-1 x 100%.
- Step 2: Sum those percentage rates.
- Step 3: Then divide by the periods.
That arithmetic average gives a feel of growth that is average. It is easy and it does not take into account the compounding since it merely averages the percentages.
Example: A firm brings in revenue of 100$ in year one, 150$ in year two and 180$ in year three. The year-to-year growth rates are:
- Year1→2: (150–100)/100 * 100% = 50%
- Year2→3: (180–150)/150 * 100% = 20%
The AAGR = (50% + 20%) / 2 = 35% per year.
It is simple to calculate yet, it is important to remember that AAGR is nothing more than the average of rates. Most applicable as a rough, and speedy indicator of multi-period growth. It is, however, misleading when there are wide fluctuations in growth as it will balance with a few large fluctuations as well as small changes. As we invest over long distances or long periods of time, the Compound Annual Growth Rate (CAGR) (below) is more often going to be more illuminating.
Compound Annual Growth Rate (CAGR)
The Compound Annual Growth Rate (CAGR) is the smooth growth rate of a period, supposing that the quantity increased at a constant compound rate of increase in every year of the period. The answer to this is: Assuming that an investment or measurement increased at a constant rate every year, what would be the constant rate to go from the initial value to the final value? The formula is:
CAGR = [(Ending Value / Beginning Value)^(1/years) – 1] * 100%.Steps to calculate CAGR:
- Divide the final value by the initial value.
- Let the outcome be to the power (1/number of years).
- Subtract 1.
- Multiply by 100 to convert to a percentage.
This is the calculation of the geometric average per annum growth. It averages unstable annual fluctuations because it assumes that there is reinvestment within a period.
Example: Consider a scenario in which one is planning to invest $10,000 in an instrument. After 3 years, the account is $19,000. To find the CAGR:
- Initial Value (BV) = 10000, Final Value (EV) = 19000, number of years = 3.
- EV/BV = 1.9.
- Take the cube root: 1.9^(1/3) ≈ 1.2386.
- Subtract 1 and multiply by 100%: (1.2386 – 1) × 100% ≈ 23.86%.
Thus, the investment’s CAGR was about 23.9% per year, even though the annual returns varied.
CAGR is commonly applied in the comparison of the growth of investments or revenues over several years. As an example, an investor invested in Amazon stock of 64,900 and it increased in value to 176,000 in 3 years, then the CAGR of [(176000/64900)/(1/3)-1)x100%] will be 39.5%. Applicability of CAGR: This formula is particularly helpful when a single annual growth rate is required to compare different investments or also in long-term growth of a project.
Monthly Growth Rate
This is the same with shorter cycles such as months. Compounder formula: in order to determine a monthly growth, an equivalent formula without exponents is used with n being months. In the case where you have values on a monthly basis the monthly compound rate is:
Monthly Growth Rate = [(End Value / Start Value)^(1/n) – 1] * 100%,where n is the number of months.
Instead, in case you have a rate per annum and desire the rate per month, use:
Monthly Rate = (1 + AnnualRate)^(1/12) – 1:contentReference[oaicite:22]{index=22}.
To illustrate, a 5 percent growth per annum translates to (1.05)^(1/12)-1 ≈ 0.407% per month. Or alternatively, when sales increased between 10,000 and 11,000 in 3 months, the growth rate will be (11000/10000)^(1/3) – 1 ≈ 3.23% per month.
Revenue Growth Rate
A revenue growth rate is simply the level of growth that has been multiplied by the revenue amount of a company. Take the exact same growth formula of percentage and apply that on sales or income values. For example, if a company’s quarterly revenue goes from $1,000,000 to $1,200,000, the revenue growth rate is (1,200,000 – 1,000,000)/1,000,000 × 100% = 20%. Tracking revenue growth is crucial: it indicates how fast a business is expanding its sales. Strong revenue growth (normally a percentage in the higher, possibly double-digit, numbers in the case of tech or startups) could be an indication of a healthy business, and declining or negative revenue growth could be a red flag to prospective investors.
The rate of revenue growth is very frequently issued as a report by the firm. To give an illustration, Our Experts states that revenue growth illustrates the total increase of income during the given period, and, therefore, tracking the revenue growth will aid in strategic decision making and raise the company’s valuation. Practically one of the prominent practices of measurement is to calculate growth on a quarterly or year- to-year basis in revenue to determine its performance.
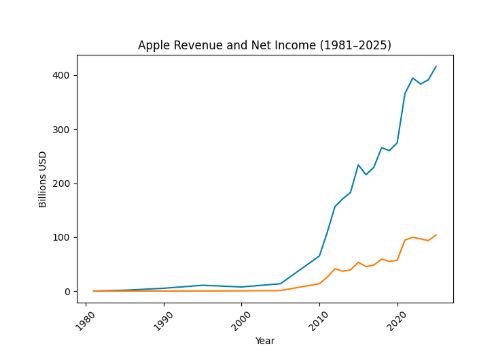
Apple’s Historical Revenue Graph
Apple’s historical revenue (blue line) and earnings (orange line) from 1981–2025 in millions USD. This graph indicates the more detailed progress of Apple’s control over its revenues in decades. The blue curve’s steep rise in the late 2000s illustrates compounding growth. To give an example, the revenue of Apple in a single year, 1999 was approximately 6,134 million, which increased to $416.2 billion in the year 2025. A compounded annual growth rate of approximately 538.14% over these years.
In comparison, the initial years are even flatter: in 1981 and 1988, the revenue was only 335 million and 4,071 million, respectively, which was growing slower, at least at the beginning. This is an illustration of how the rate of compound growth more than 20% per annum could increase the sales of a firm by a significant margin with time. Such visual charts can be used to compare growth trends and emphasize the rationale behind knowing the appropriate growth-rate formula when analyzing a business.
Using a Growth Rate Calculator
The growth rate can be manually calculated by hand, but the online tools can be used to make this considerably faster when the growth rate is complex. To provide an example, the Growth Rate Calculator that Databox has will only require you to put in a starting and ending price, this will automatically calculate the growth rate in percentages. Our calculators have the formulas of the above incorporated to allow you to get your calculator in a few seconds. Most analytics software and in-spreadsheet applications Excel, Google Sheets, etc. even include their own CAGR formula and percentage growth formula on the platform.
Frequently Asked Questions
Q: How do I calculate a growth rate between two values?
A: Now take the difference between the value and subtract the old and add the new value to obtain the change divided by the old value multiplied by 100 to obtain a percentage. In formula form: ((New – Old)/Old)x100%. The following applies to any given one-time change (year-over-year, month-over-month, etc.). As an illustration, a growth of 20 percent can be obtained with 120K compared to 100K.
Q: What’s the difference between CAGR and average growth rate?
A: CAGR presupposes that there is compounding and it provides a smoothed average annual rate on a multi-year basis. A simple mean of the growth rates of each year is simply the average (AAGR). When estimating the value of investment or when smoothing the volatile data, go with CAGR since the value is used to indicate the growth of the compound. When it does not matter whether we are dealing with a compound or not, use average growth, which is quick and rough.
Q: Can a growth rate be negative or over 100%?
A: Yes, A negative rate of growth would merely indicate a decline (e.g. -10% would indicate that the value decreased 10%). The value increased more than two times, a growth rate of over 100%. An example of this would be the growth of 100 to 250, a 150 percent increase. The formulae permit any outcome, interpretation depends upon the context.
Q: When should I use CAGR instead of simple growth?
A: CAGR should be used in comparing performance in many periods or making a projection under compound conditions. Preferably, it is when returns are reinvested or when growth is based on previous growth. Single growth is adequate during a single time duration or where compounding is not taken.
Conclusion
Business analysis and investment require an understanding of how to determine growth rate. We have discussed the basic growth metrics: the percent interval growth formula for one-period and the average growth rate (AAGR), that is, simple multi-period trend and one-year average growth rate (AAGR) for smoothing out multi-year human performance. They all have applications but basic growth should be used to get a quick comparison, average growth can be used to do some general trending and CAGR should be used as a year-over-year comparison. We even learned how to deal with special cases such as monthly growth and growth specific to revenue.
Practically, it is always required to indicate which growth formula to apply and why. As an example, one might mention a CAGR in which one desires to demonstrate the smoothed historical long-run operation of revenue or investment. To not make errors, calculate step-by-step or use dice roll growth rate calculators.
By these formulas, as well as concepts, the business people and students will be in a position to make accurate estimates of growth and explain it accurately, be it forecasting, investment or even trending. To have more practice, combine your numbers within a growth rate calculator or a spreadsheet and determine whether the above steps work. The ease of growth rate use will make you make a decision that will lead to financial independence as well as interpret your findings based on the information results.
Leave a Reply